Statistical & Financial Consulting by Stanford PhD
Home Page
JUMP-DIFFUSION
 = A(t,X(t)) dt + B(t,X(t)) dW(t) + C(t,X(t)) dN(t),)
where)
is an n-dimensional vector,
)
is an n-by-m matrix,
)
is an n-by-r matrix,
)
is an m-dimensional Brownian motion and
)
is an r-dimensional counting process. In other words, jump-diffusions are solutions of stochastic differential equations containing stochastic integrals with respect Brownian motion and various jump processes. One particular specification is illustrated below.
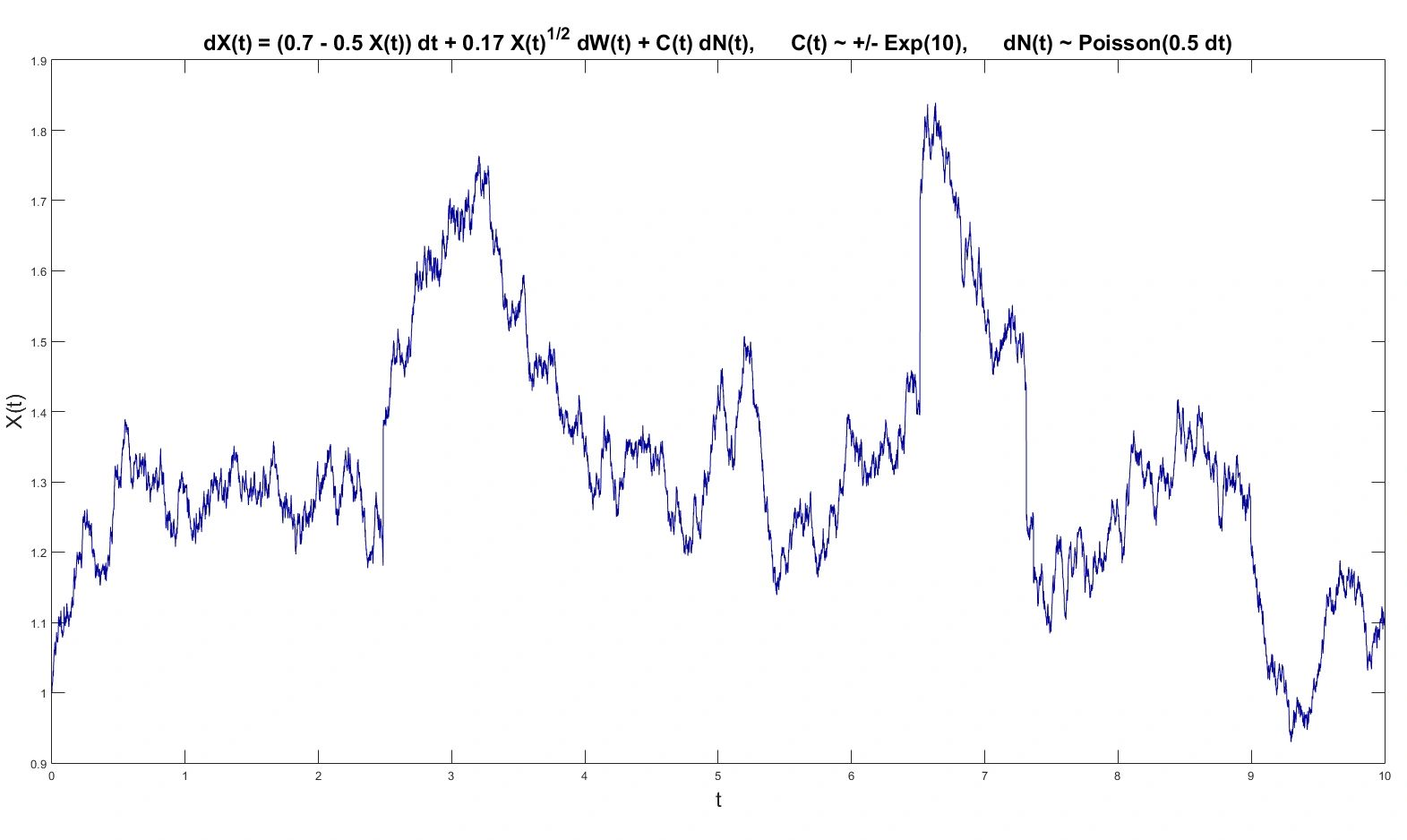
Properties of jump-diffusions are an integral part of stochastic calculus. Several important models in empirical finance, financial engineering, engineering and physics are phrased in terms of jump-diffusions.
JUMP-DIFFUSION REFERENCES
Karatzas, I., & Shreve, S. E. (1991). Brownian Motion and Stochastic Calculus (2nd ed). New York: Springer.
Shreve, S. E. (2004). Stochastic Calculus for Finance II: Continuous-Time Models. New York: Springer.
Oksendal, B. K. (2002). Stochastic Differential Equations: An Introduction with Applications (5th ed). Springer.
Protter, P. E. (2005). Stochastic Integration and Differential Equations (2nd ed). Springer.
Gikhman, I. I., & Skorokhod, A. V. (2007). The Theory of Stochastic Processes III. Springer.
BACK TO THE STATISTICAL ANALYSES DIRECTORY
IMPORTANT LINKS ON THIS SITE
Jump-diffusion is an n-dimensional stochastic process
satisfying the following stochastic differential equation (SDE):
where
Properties of jump-diffusions are an integral part of stochastic calculus. Several important models in empirical finance, financial engineering, engineering and physics are phrased in terms of jump-diffusions.
JUMP-DIFFUSION REFERENCES
Karatzas, I., & Shreve, S. E. (1991). Brownian Motion and Stochastic Calculus (2nd ed). New York: Springer.
Shreve, S. E. (2004). Stochastic Calculus for Finance II: Continuous-Time Models. New York: Springer.
Oksendal, B. K. (2002). Stochastic Differential Equations: An Introduction with Applications (5th ed). Springer.
Protter, P. E. (2005). Stochastic Integration and Differential Equations (2nd ed). Springer.
Gikhman, I. I., & Skorokhod, A. V. (2007). The Theory of Stochastic Processes III. Springer.
BACK TO THE STATISTICAL ANALYSES DIRECTORY
IMPORTANT LINKS ON THIS SITE
- Detailed description of the services offered in the areas of statistical consulting and financial consulting: home page, types of service, experience, case studies and payment options
- Directory of financial topics