Statistical & Financial Consulting by Stanford PhD
Home Page
NAIVE BAYES
 = \frac{\prod_{j = 1,..., J} f_{jk}(x_j) p_k}{\sum_{l = 1,...,K} \prod_{j = 1,..., J} f_{jl}(x_j) p_l},\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \textbf{(1)})
where
are unconditional probabilities of each class. The unconditional probabilities can be estimated as the sample frequencies or stipulated using some prior knowledge. The data point is classified to class
for which probability (1) is highest.
Naive Bayes performs well in many settings but fails completely in situations where the classes are distinguished by the codependency structure of
An example is visualized below.
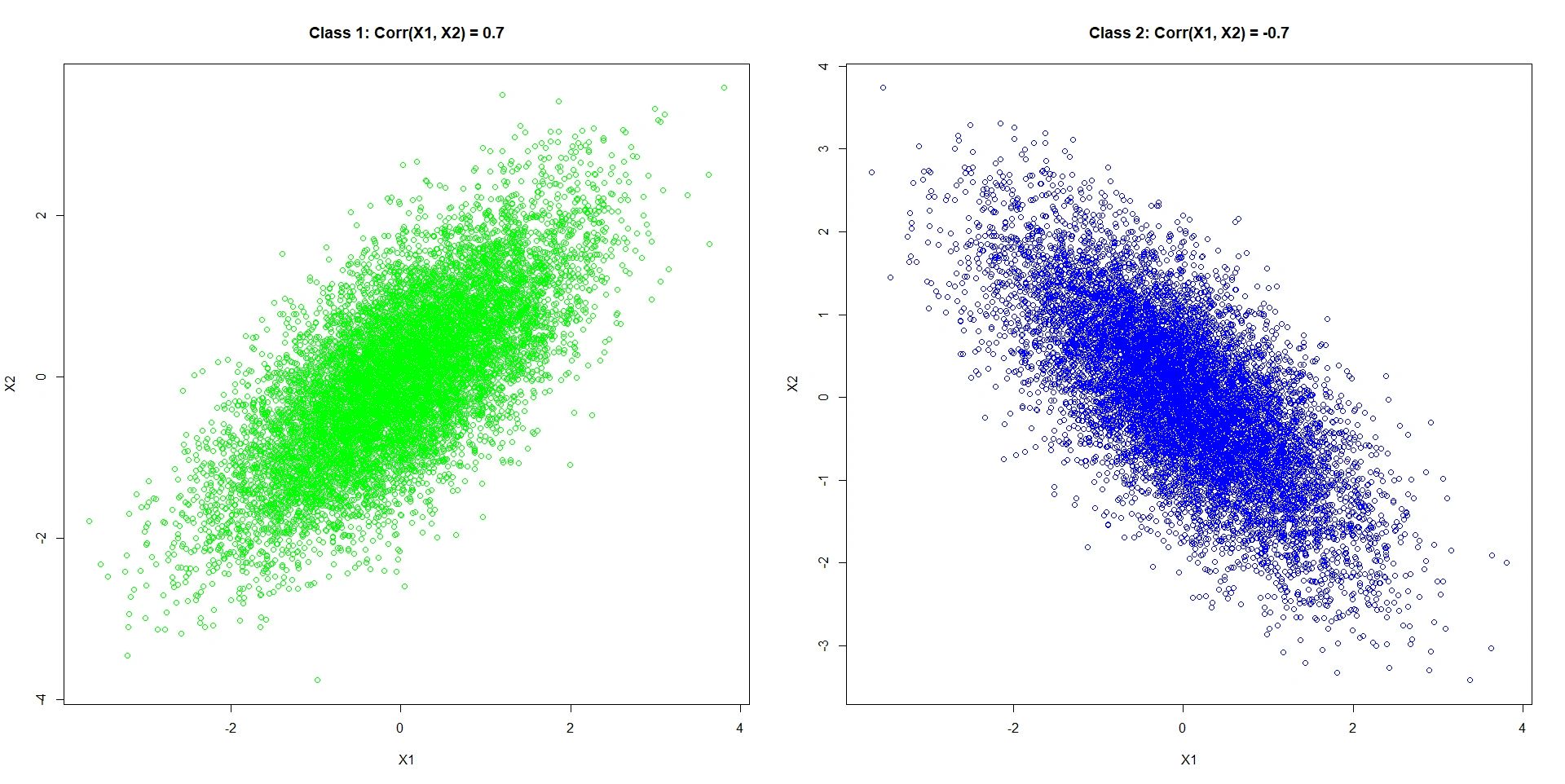
Here the two variables
and
are normally distributed with mean 0 and standard deviation 1. The only thing which is different between the classes is how the variables relate to each other.
NAIVE BAYES REFERENCES
Barber, D. (2014). Bayesian Reasoning and Machine Learning. Cambridge University Press.
Han, J., Kamber, M. & Pei, J. (2012). Data mining: Concepts and Techniques (3rd ed). Morgan-Kaufman.
Hastie, T., Tibshirani, R., & Friedman, J. H. (2008). The elements of statistical learning: Data mining, inference, and prediction. New York: Springer.
Bishop, C. M. (2006) Pattern Recognition and Machine Learning. New York: Springer.
Witten, I. H., Frank, E., Hall, M., A., & Pal, C. J. (2017). Data Mining: Practical Machine Learning Tools and Techniques (4th ed). New York: Morgan-Kaufmann.
Duda, R. O., Hart, P. E., & Stork, D. G. (2000). Pattern Classification (2nd ed). New York: Wiley-Interscience.
BACK TO THE STATISTICAL ANALYSES DIRECTORY
IMPORTANT LINKS ON THIS SITE
Naive Bayes is a classification method. Suppose the data are split into
classes and we observe
variables
We conveniently assume that in each class the variables are independent (hence the term "naive"). We estimate densities of the continuous variables and probability mass functions of the discrete variables as
in each class
Then, whenever we see a data point with unknown class membership and known
we apply the Bayes rule. We estimate the probability of class
membership as
where
Naive Bayes performs well in many settings but fails completely in situations where the classes are distinguished by the codependency structure of
Here the two variables
NAIVE BAYES REFERENCES
Barber, D. (2014). Bayesian Reasoning and Machine Learning. Cambridge University Press.
Han, J., Kamber, M. & Pei, J. (2012). Data mining: Concepts and Techniques (3rd ed). Morgan-Kaufman.
Hastie, T., Tibshirani, R., & Friedman, J. H. (2008). The elements of statistical learning: Data mining, inference, and prediction. New York: Springer.
Bishop, C. M. (2006) Pattern Recognition and Machine Learning. New York: Springer.
Witten, I. H., Frank, E., Hall, M., A., & Pal, C. J. (2017). Data Mining: Practical Machine Learning Tools and Techniques (4th ed). New York: Morgan-Kaufmann.
Duda, R. O., Hart, P. E., & Stork, D. G. (2000). Pattern Classification (2nd ed). New York: Wiley-Interscience.
BACK TO THE STATISTICAL ANALYSES DIRECTORY
IMPORTANT LINKS ON THIS SITE
- Detailed description of the services offered in the areas of statistical and financial consulting: home page, types of service, experience, case studies, payment options and statistics tutoring
- Directory of financial topics