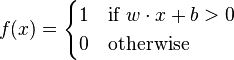Statistical & Financial Consulting by Stanford PhD
Home Page
NEURAL NETWORK

Artificial Neural Network (artificial neural net) is a multi-layer nonlinear modeling procedure which exploits a large set of variables. It is designed to reveal hidden complex relationships in the data.  Term "neural network" may also refer to a specific multi-layer nonlinear function which  represents one or more dependent variables in terms of many independent variables. The dependent variables are known as the output values of the neural network, and the independent variables are known as the input values. Neural nets are used for both regression and classification. In the regression setting the dependent variable is continuous and we model its variation with the help of independent variables. In the classification setting the independent variables are used to determine the probabilities for the K possible categories of a given object. The true category of the object is stored in the dependent variable.

The shape of an artificial neural network mimics that of a neural network of a human brain. That is the rationale for the name. An artificial neural network is composed of layers of neurons, which act as nodes in the network. The first layer is the input layer of neurons. It receives input signals (values). The last layer is the output layer of neurons. It produces the output signals (values). In-between there are multiple "hidden" layers of neurons. Each neuron in the network receives signals (values) from several neurons in the previous layer, transforms them and then sends the same signal (value) to several neurons in the next layer. In the neuron, the aggregation of the signals received from the previous layer is linear. The signals are summed up with different weights. The transformation of the aggregated signals is where the novelty is introduced. Typically, the transformation is a highly non-linear function. So the distribution of the output does not resemble the distribution of the input. Still, the transformation may be a simple function. One example is perceptron, which is defined by the following rule:

f(x) = \begin{cases}1 & \text{if }w \cdot x + b > 0\\0 & \text{otherwise}\end{cases}

Perceptrons replicate exactly what a human brain does. A neuron passes the signals further only if their cumulative magnitude exceeds a certain threshold. The idea is sound and has reflection in many parts of life. There is only one minor flaw. The resulting neural network is a discontinuous function of the parameters. This leads to any error function being a discontinuous function of the parameters as well. The error function measures the discrepancy between the predictions of the neural network and the truth on a given training data set. We would want the error function to be continuous in parameters, which is necessary for several estimation methods. Therefore, in real applications perceptrons are approximated arbitrarily well with continuous functions called sigmoids. This approximation makes the whole network continuous in both parameters and inputs.

The estimation of the parameters is typically done in an iterative fashion. One method is called back-propagation. It works in the following way. At the beginning of each iteration, we have an estimate of the parameters calculated at the previous iteration. We decompose the gradient of the error function with respect to the parameters into pieces corresponding to different nodes (neurons). This is possible due to the chain rule. We have pre-calculated values of those pieces from the previous iteration. Now we perform two steps. In the forward step, we assemble the gradient pieces to calculate the gradient. We multiply the gradient by a constant learning rate and use the product to update the estimate of the parameters. Using the new estimate, we propagate the input values forward through each node (neuron) and calculate the new values of the nodes as well as the new output values. The new output values lead to new errors when compared against the truth. In the backward step, we propagate these new errors back through each node to calculate the pieces of the gradient corresponding to each node. And then a new iteration begins... For a formal definition of the back-propagation algorithm as well as its properties, see the references.

Neural nets are employed in construction of artificial intelligence algorithms in robotics, healthcare and finance. One example: using multiple inputs, model a decision making process in the brain of a practicing M.D. Namely, using all kinds of data on a given patient, model the process of giving a diagnosis to the patient. Another example: use neural nets to pick up any relationships in the stock market for the purpose of proprietary trading.

Over the last 15 years, it has been established that if we keep the total number of nodes large and fixed, then deep neural nets (many layers, relatively few nodes per layer) perform much better than shallow nets (few layers, relatively many nodes per layer) on many image processing and text mining tasks. This has led to explosion of the field of deep learning. Nowadays, all major industry-based artificial intelligence laboratories have dedicated deep learning effort. For example, the Google Brain team is responsible for developing an open and extensive implementation of deep learning methods in Python and C, known as TensorFlow (there are APIs from TensorFlow to some other programming languages as well: C++, C#, Java, etc).


NEURAL NETWORK REFERENCES
Bishop, C. M (1996). Neural Networks for Pattern Recognition. Oxford University Press.

Mandic, D. & Chambers, J. (2001). Recurrent Neural Networks for Prediction: Architectures, Learning algorithms and Stability. Wiley.

Hastie, T., Tibshirani, R., & Friedman, J. H. (2008). The elements of statistical learning: Data mining, inference, and prediction. New York: Springer.

Pregibon, D. (1997). Data Mining. Statistical Computing and Graphics, 7, 8.

Westphal, C., Blaxton, T. (1998). Data mining solutions. New York: Wiley.

Witten, I. H., Frank, E., Hall, M., A., Pal, & C. J. (2017). Data Mining: Practical Machine Learning Tools and Techniques (4th ed). New York: Morgan-Kaufmann.

Duda, R. O., Hart, P. E., & Stork, D. G. (2000). Pattern Classification (2nd ed). New York: Wiley-Interscience.

Efron, B., & Hastie, T. (2017). Computer Age Statistical Inference: Algorithms, Evidence, and Data Science. Cambridge University Press.

Goodfellow, I., Bengio. Y., & Courville. A. (2016). Deep Learning. MIT Press.
 

NEURAL NETWORK RESOURCES
BACK TO THE STATISTICAL ANALYSES DIRECTORY


IMPORTANT LINKS ON THIS SITE